A model of language learning

lecture

Date

23 April 2024

Modified

7 May 2024

Update 7 May 2024

Fixed bug in the learn! function so that learning also occurs on strings in the intersection \(L_1 \cap L_2\) of the two languages.

Update 30 April 2024

Fixed the set diagrams for \(L_1 \setminus L_2\) and \(L_2 \setminus L_1\).

Plan

Starting this week, we will put programming to good use
We’ll start with a simple model of language learning
- Here, learning = process of updating a linguistic representation
- Doesn’t matter whether child or adult

Grammar competition

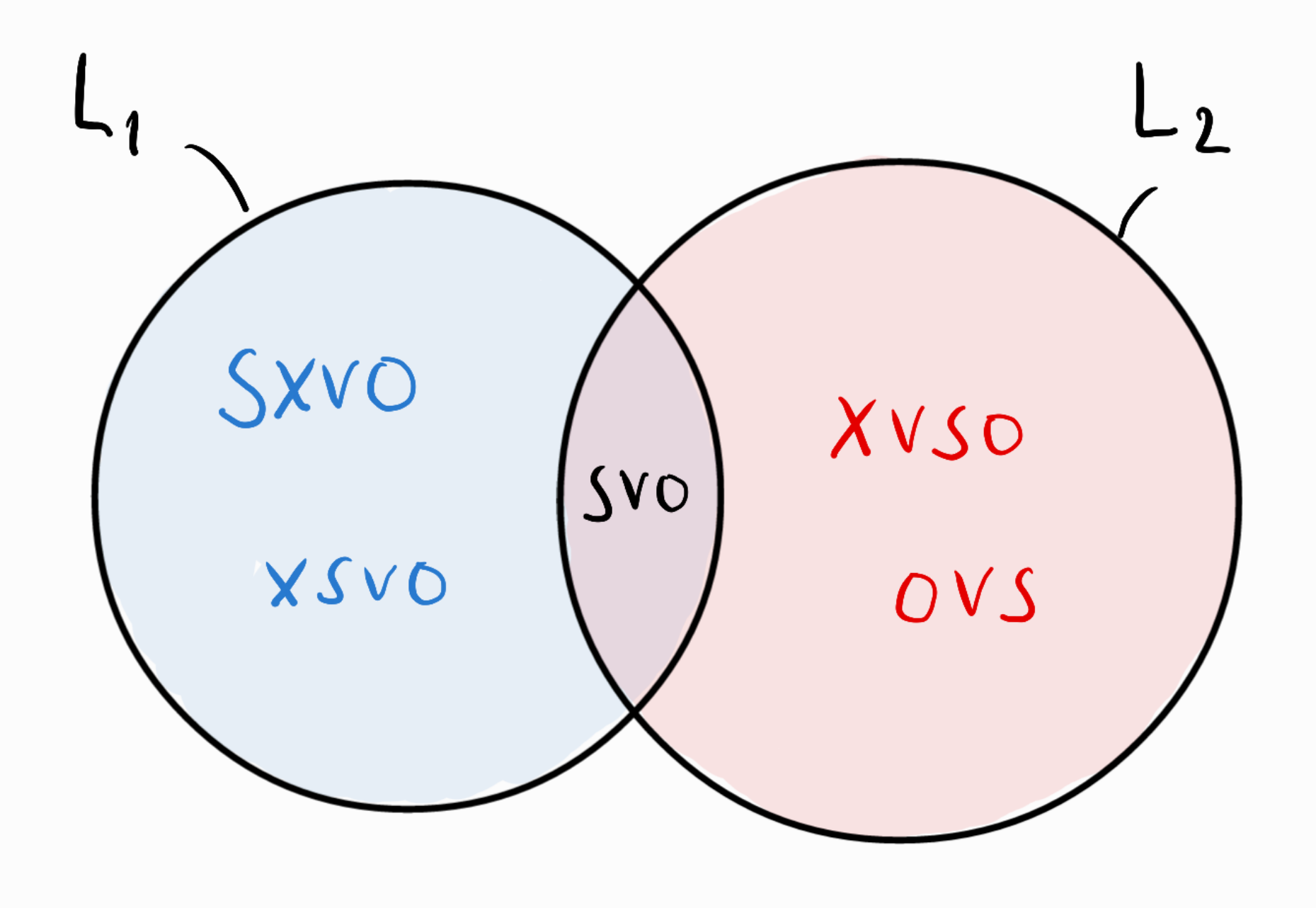
Assume two grammars \(G_1\) and \(G_2\) that generate languages \(L_1\) and \(L_2\)
- language = set of strings (e.g. sentences)
In general, \(L_1\) and \(L_2\) will be different but may overlap:

Grammar competition

Three sets of interest: \(L_1 \setminus L_2\), \(L_1 \cap L_2\) and \(L_2 \setminus L_1\)

Concrete example

SVO (\(G_1\)) vs. V2 (\(G_2\))

Grammar competition

Suppose learner receives randomly chosen strings from \(L_1\) and \(L_2\)
Learner uses either \(G_1\) or \(G_2\) to parse incoming string
Define \(p =\) probability of use of \(G_1\)
How should the learner update \(p\) in response to interactions with his/her environment?

Variational learning

Suppose learner receives string/sentence \(s\)
Then update is:

Learner’s grammar	String received	Update
\(G_1\)	\(s \in L_1\)	increase \(p\)
\(G_1\)	\(s \in L_2 \setminus L_1\)	decrease \(p\)
\(G_2\)	\(s \in L_2\)	decrease \(p\)
\(G_2\)	\(s \in L_1 \setminus L_2\)	increase \(p\)

Exercise

How can we increase/decrease \(p\) in practice? What is the update formula?

Answer

One possibility (which we will stick to):

Increase: \(p\) becomes \(p + \gamma (1 - p)\)
Decrease: \(p\) becomes \(p - \gamma p\)

The parameter \(0 < \gamma < 1\) is a learning rate

Why this form of update formula?

Need to make sure that always \(0 \leq p \leq 1\) (it is a probability)
Also notice:
- When \(p\) is increased, what is added is \(\gamma (1-p)\). Since \(1-p\) is the probability of \(G_2\), this means transferring an amount of the probability mass of \(G_2\) onto \(G_1\).
- When \(p\) is decreased, what is removed is \(\gamma p\). Since \(p\) is the probability of \(G_1\), this means transferring an amount of the probability mass of \(G_1\) onto \(G_2\).
- Learning rate \(\gamma\) determines how much probability mass is transferred.

Plan

To implement a variational learner computationally, we need:
1. A representation of a learner who embodies a single probability, \(p\), and a learning rate, \(\gamma\)
2. A way to sample strings from \(L_1 \setminus L_2\) and from \(L_2 \setminus L_1\)
3. A function that updates the learner’s \(p\)
Let’s attempt this now!

The struct

The first point is very easy:

mutable struct VariationalLearner
  p::Float64
  gamma::Float64
end

Sampling strings

For the second point, note we have three types of strings which occur with three corresponding probabilities
Let’s refer to the string types as "S1", "S12" and "S2", and to the probabilities as P1, P12 and P2:

String type	Probability	Explanation
`"S1"`	`P1`	\(s \in L_1 \setminus L_2\)
`"S12"`	`P12`	\(s \in L_1 \cap L_2\)
`"S2"`	`P2`	\(s \in L_2 \setminus L_1\)

In Julia, sampling from a finite number of options (here, three string types) with corresponding probabilities is handled by a function called sample() which lives in the StatsBase package
First, install and load the package:

using Pkg
Pkg.add("StatsBase")
using StatsBase

Now to sample a string, you can do the following:

# the three probabilities (just some numbers I invented)
P1 = 0.4
P12 = 0.5
P2 = 0.1

# sample one string
sample(["S1", "S12", "S2"], Weights([P1, P12, P2]))

"S12"

Tidying up

The above works but is a bit cumbersome – for example, every time you want to sample a string, you need to refer to the three probabilities
Let’s carry out a bit of software engineering to make this nicer to use
First, we encapsulate the probabilities in a struct of their own:

struct LearningEnvironment
  P1::Float64
  P12::Float64
  P2::Float64
end

We then define the following function:

function sample_string(x::LearningEnvironment)
  sample(["S1", "S12", "S2"], Weights([x.P1, x.P12, x.P2]))
end

sample_string (generic function with 1 method)

Test the function:

paris = LearningEnvironment(0.4, 0.5, 0.1)
sample_string(paris)

"S12"

Implementing learning

We now need to tackle point 3, the learning function which updates the learner’s state
This needs to do three things:
1. Sample a string from the learning environment
2. Pick a grammar to try and parse the string with
3. Update \(p\) in response to whether parsing was successful or not

Exercise

How would you implement point 2, i.e. picking a grammar to try and parse the incoming string?

Answer

We can again use the sample() function from StatsBase, and define:

function pick_grammar(x::VariationalLearner)
  sample(["G1", "G2"], Weights([x.p, 1 - x.p]))
end

pick_grammar (generic function with 1 method)

Implementing learning

Now it is easy to implement the first two points of the learning function:

function learn!(x::VariationalLearner, y::LearningEnvironment)
  s = sample_string(y)
  g = pick_grammar(x)
end

learn! (generic function with 1 method)

How to implement the last point, i.e. updating \(p\)?

Aside: conditional statements

Here, we will be helped by conditionals:

if COND1
  # this is executed if COND1 is true
elseif COND2
  # this is executed if COND1 is false but COND2 is true
else
  # this is executed otherwise
end

Note: only the if block is necessary; elseif and else are optional, and there may be more than one elseif block

Aside: conditional statements

Try this for different values of number:

number = 1

if number > 0
  println("Your number is positive!")
elseif number < 0
  println("Your number is negative!")
else
  println("Your number is zero!")
end

Comparison \(\neq\) assignment

Important

To compare equality of two values inside a condition, you must use a double equals sign, ==. This is because the single equals sign, =, is already reserved for assigning values to variables.

if 0 = 1    # throws an error!
  println("The world is topsy-turvy")
end

if 0 == 1   # works as expected
  println("The world is topsy-turvy")
end

Exercise

Use an if ... elseif ... else ... end block to finish off our learn! function
Tip: logical “and” is &&, logical “or” is ||
Recall:

Learner’s grammar	String received	Update
\(G_1\)	\(s \in L_1\)	increase \(p\)
\(G_1\)	\(s \in L_2 \setminus L_1\)	decrease \(p\)
\(G_2\)	\(s \in L_2\)	decrease \(p\)
\(G_2\)	\(s \in L_1 \setminus L_2\)	increase \(p\)

Answer

Important! The following function, which we originally used, has a bug! It does not update the learner’s state with input strings from \(L_1 \cap L_2\). See below for fixed version.

function learn!(x::VariationalLearner, y::LearningEnvironment)
  s = sample_string(y)
  g = pick_grammar(x)

  if g == "G1" && s == "S1"
    x.p = x.p + x.gamma * (1 - x.p)
  elseif g == "G1" && s == "S2"
    x.p = x.p - x.gamma * x.p
  elseif g == "G2" && s == "S2"
    x.p = x.p - x.gamma * x.p
  elseif g == "G2" && s == "S1"
    x.p = x.p + x.gamma * (1 - x.p)
  end

  return x.p
end

Answer

function learn!(x::VariationalLearner, y::LearningEnvironment)
  s = sample_string(y)
  g = pick_grammar(x)

  if g == "G1" && s != "S2"
    x.p = x.p + x.gamma * (1 - x.p)
  elseif g == "G1" && s == "S2"
    x.p = x.p - x.gamma * x.p
  elseif g == "G2" && s != "S1"
    x.p = x.p - x.gamma * x.p
  elseif g == "G2" && s == "S1"
    x.p = x.p + x.gamma * (1 - x.p)
  end

  return x.p
end

learn! (generic function with 1 method)

Testing our code

Let’s test our code!

bob = VariationalLearner(0.5, 0.01)
paris = LearningEnvironment(0.4, 0.5, 0.1)

learn!(bob, paris)
learn!(bob, paris)
learn!(bob, paris)
learn!(bob, paris)
learn!(bob, paris)

0.51489901495

trajectory = [learn!(bob, paris) for t in 1:1000]

1000-element Vector{Float64}:
 0.5097500248005
 0.514652524552495
 0.5195059993069701
 0.5143109393139004
 0.5191678299207614
 0.5239761516215538
 0.5287363901053382
 0.5334490262042848
 0.5381145359422419
 0.5327333905828194
 0.5374060566769913
 0.5420319961102213
 0.5466116761491191
 ⋮
 0.8043883364948524
 0.7963444531299039
 0.7983810085986048
 0.7903971985126188
 0.7924932265274927
 0.7945682942622178
 0.7966226113195956
 0.7986563852063996
 0.7906698213543356
 0.7927631231407922
 0.7948354919093843
 0.7968871369902905

Plotting the learning trajectory

using Plots
plot(1:1000, trajectory)

Bibliographical remarks

For more about the notion of grammar competition, see Kroch (1989), Kroch (1994)
Variational learner originally from Yang (2000), Yang (2002)
Learning algorithm itself is old: Bush and Mosteller (1955)

Summary

You’ve learned a few important concepts today:
- Grammar competition and variational learning
- How to sample objects according to a discrete probability distribution
- How to use conditional statements
- How to make a simple plot of a learning trajectory
You get to practice these in the homework
Next week, we’ll take the model to a new level and consider what happens when several variational learners interact

References

Bush, Robert R., and Frederick Mosteller. 1955. Stochastic Models for Learning. New York, NY: Wiley.

Kroch, Anthony S. 1989. “Reflexes of Grammar in Patterns of Language Change.” Language Variation and Change 1 (3): 199–244. https://doi.org/10.1017/S0954394500000168.

———. 1994. “Morphosyntactic Variation.” In Proceedings of the 30th Annual Meeting of the Chicago Linguistic Society, edited by K. Beals, 180–201. Chicago, IL: Chicago Linguistic Society.

Yang, Charles D. 2000. “Internal and External Forces in Language Change.” Language Variation and Change 12: 231–50. https://doi.org/10.1017/S0954394500123014.

———. 2002. Knowledge and Learning in Natural Language. Oxford: Oxford University Press.

Other Formats

Plan

Grammar competition

Grammar competition

Concrete example

Grammar competition

Variational learning

Exercise

Why this form of update formula?

Plan

The struct

Sampling strings

Tidying up

Implementing learning

Exercise

Implementing learning

Aside: conditional statements

Aside: conditional statements

Comparison \(\neq\) assignment

Exercise

Testing our code

Plotting the learning trajectory

Bibliographical remarks

Summary

References