A model of language learning
Agent-based modelling, Konstanz, 2024
23 April 2024
Plan
- Starting this week, we will put programming to good use
- We’ll start with a simple model of language learning
- Here, learning = process of updating a linguistic representation
- Doesn’t matter whether child or adult
Grammar competition
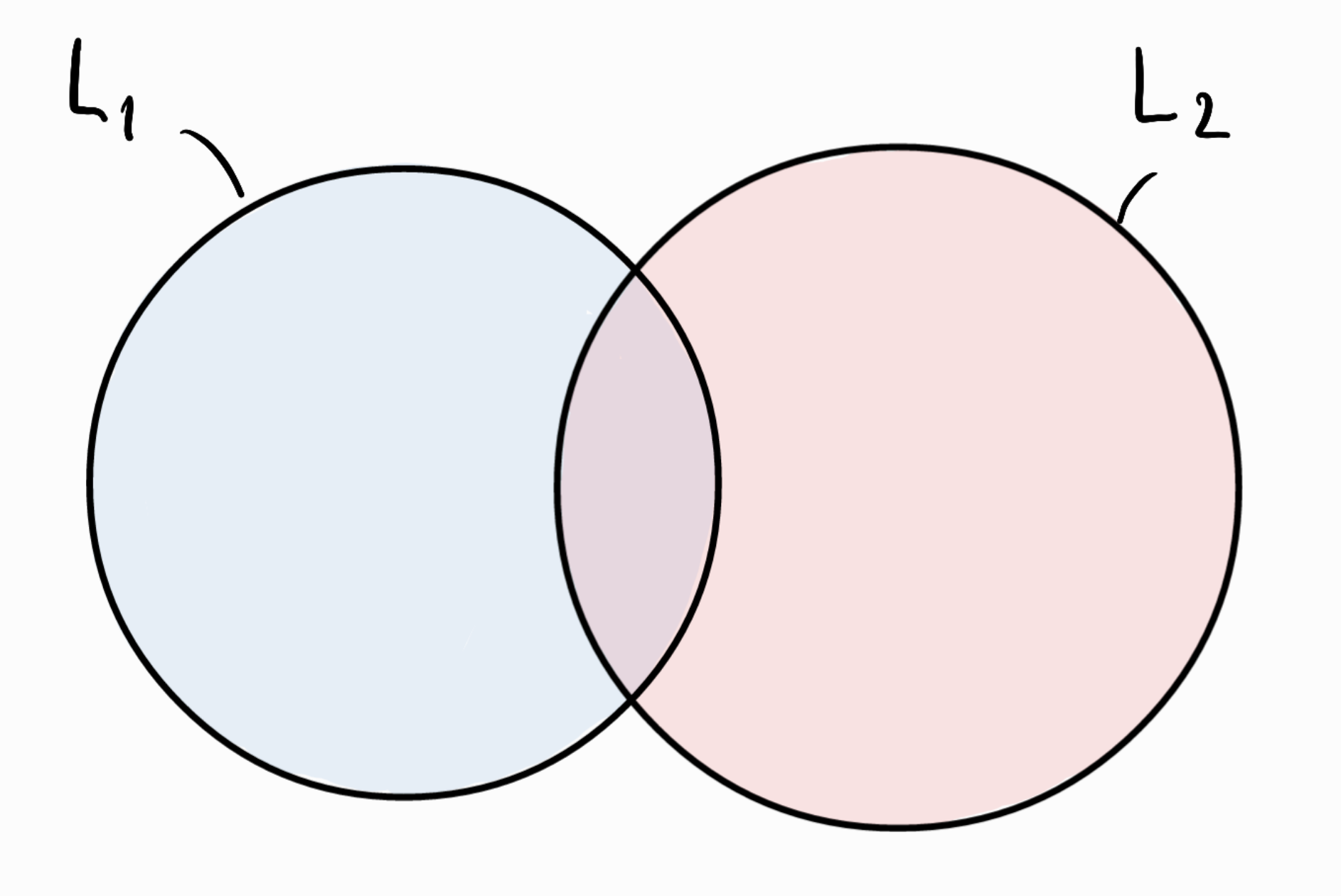
- Assume two grammars \(G_1\) and \(G_2\) that generate languages \(L_1\) and \(L_2\)
- language = set of strings (e.g. sentences)
- In general, \(L_1\) and \(L_2\) will be different but may overlap:
Grammar competition
- Three sets of interest: \(L_1 \setminus L_2\), \(L_1 \cap L_2\) and \(L_2 \setminus L_1\)

Grammar competition
- Three sets of interest: \(L_1 \setminus L_2\), \(L_1 \cap L_2\) and \(L_2 \setminus L_1\)

Grammar competition
- Three sets of interest: \(L_1 \setminus L_2\), \(L_1 \cap L_2\) and \(L_2 \setminus L_1\)

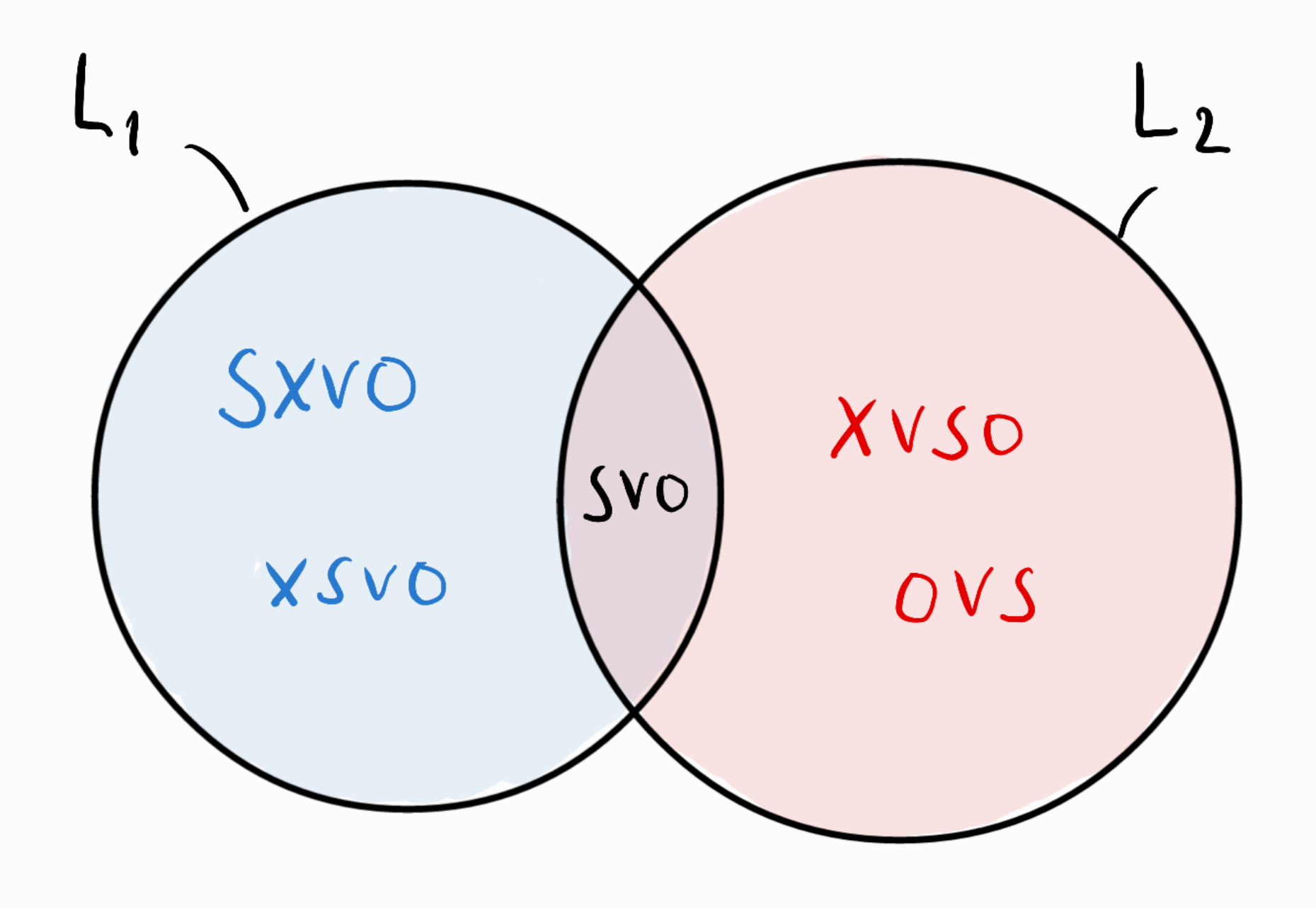
Concrete example
- SVO (\(G_1\)) vs. V2 (\(G_2\))
Grammar competition
- Suppose learner receives randomly chosen strings from \(L_1\) and \(L_2\)
- Learner uses either \(G_1\) or \(G_2\) to parse incoming string
- Define \(p =\) probability of use of \(G_1\)
- How should the learner update \(p\) in response to interactions with his/her environment?
Variational learning
- Suppose learner receives string/sentence \(s\)
- Then update is:
| Learner’s grammar | String received | Update |
|---|---|---|
| \(G_1\) | \(s \in L_1\) | increase \(p\) |
| \(G_1\) | \(s \in L_2 \setminus L_1\) | decrease \(p\) |
| \(G_2\) | \(s \in L_2\) | decrease \(p\) |
| \(G_2\) | \(s \in L_1 \setminus L_2\) | increase \(p\) |
Exercise
How can we increase/decrease \(p\) in practice? What is the update formula?
Exercise
Answer
One possibility (which we will stick to):
- Increase: \(p\) becomes \(p + \gamma (1 - p)\)
- Decrease: \(p\) becomes \(p - \gamma p\)
The parameter \(0 < \gamma < 1\) is a learning rate
Why this form of update formula?
- Need to make sure that always \(0 \leq p \leq 1\) (it is a probability)
- Also notice:
- When \(p\) is increased, what is added is \(\gamma (1-p)\). Since \(1-p\) is the probability of \(G_2\), this means transferring an amount of the probability mass of \(G_2\) onto \(G_1\).
- When \(p\) is decreased, what is removed is \(\gamma p\). Since \(p\) is the probability of \(G_1\), this means transferring an amount of the probability mass of \(G_1\) onto \(G_2\).
- Learning rate \(\gamma\) determines how much probability mass is transferred.
Plan
- To implement a variational learner computationally, we need:
- A representation of a learner who embodies a single probability, \(p\), and a learning rate, \(\gamma\)
- A way to sample strings from \(L_1 \setminus L_2\) and from \(L_2 \setminus L_1\)
- A function that updates the learner’s \(p\)
- Let’s attempt this now!
The struct
- The first point is very easy:
Sampling strings
- For the second point, note we have three types of strings which occur with three corresponding probabilities
- Let’s refer to the string types as
"S1","S12"and"S2", and to the probabilities asP1,P12andP2:
| String type | Probability | Explanation |
|---|---|---|
"S1" |
P1 |
\(s \in L_1 \setminus L_2\) |
"S12" |
P12 |
\(s \in L_1 \cap L_2\) |
"S2" |
P2 |
\(s \in L_2 \setminus L_1\) |
Sampling strings
- In Julia, sampling from a finite number of options (here, three string types) with corresponding probabilities is handled by a function called
sample()which lives in theStatsBasepackage - First, install and load the package:
Sampling strings
Now to sample a string, you can do the following:
Tidying up
- The above works but is a bit cumbersome – for example, every time you want to sample a string, you need to refer to the three probabilities
- Let’s carry out a bit of software engineering to make this nicer to use
- First, we encapsulate the probabilities in a struct of their own:
Tidying up
- We then define the following function:
function sample_string(x::LearningEnvironment)
sample(["S1", "S12", "S2"], Weights([x.P1, x.P12, x.P2]))
endsample_string (generic function with 1 method)- Test the function:
Implementing learning
- We now need to tackle point 3, the learning function which updates the learner’s state
- This needs to do three things:
- Sample a string from the learning environment
- Pick a grammar to try and parse the string with
- Update \(p\) in response to whether parsing was successful or not
Exercise
How would you implement point 2, i.e. picking a grammar to try and parse the incoming string?
Exercise
Implementing learning
- Now it is easy to implement the first two points of the learning function:
function learn!(x::VariationalLearner, y::LearningEnvironment)
s = sample_string(y)
g = pick_grammar(x)
endlearn! (generic function with 1 method)- How to implement the last point, i.e. updating \(p\)?
Aside: conditional statements
- Here, we will be helped by conditionals:
- Note: only the
ifblock is necessary;elseifandelseare optional, and there may be more than oneelseifblock
Aside: conditional statements
- Try this for different values of
number:
Comparison \(\neq\) assignment
Important
To compare equality of two values inside a condition, you must use a double equals sign, ==. This is because the single equals sign, =, is already reserved for assigning values to variables.
Exercise
- Use an
if ... elseif ... else ... endblock to finish off ourlearn!function - Tip: logical “and” is
&&, logical “or” is|| - Recall:
| Learner’s grammar | String received | Update |
|---|---|---|
| \(G_1\) | \(s \in L_1\) | increase \(p\) |
| \(G_1\) | \(s \in L_2 \setminus L_1\) | decrease \(p\) |
| \(G_2\) | \(s \in L_2\) | decrease \(p\) |
| \(G_2\) | \(s \in L_1 \setminus L_2\) | increase \(p\) |
Exercise
Answer
Important! The following function, which we originally used, has a bug! It does not update the learner’s state with input strings from \(L_1 \cap L_2\). See below for fixed version.
function learn!(x::VariationalLearner, y::LearningEnvironment)
s = sample_string(y)
g = pick_grammar(x)
if g == "G1" && s == "S1"
x.p = x.p + x.gamma * (1 - x.p)
elseif g == "G1" && s == "S2"
x.p = x.p - x.gamma * x.p
elseif g == "G2" && s == "S2"
x.p = x.p - x.gamma * x.p
elseif g == "G2" && s == "S1"
x.p = x.p + x.gamma * (1 - x.p)
end
return x.p
endExercise
Answer
function learn!(x::VariationalLearner, y::LearningEnvironment)
s = sample_string(y)
g = pick_grammar(x)
if g == "G1" && s != "S2"
x.p = x.p + x.gamma * (1 - x.p)
elseif g == "G1" && s == "S2"
x.p = x.p - x.gamma * x.p
elseif g == "G2" && s != "S1"
x.p = x.p - x.gamma * x.p
elseif g == "G2" && s == "S1"
x.p = x.p + x.gamma * (1 - x.p)
end
return x.p
endlearn! (generic function with 1 method)Testing our code
- Let’s test our code!
Testing our code
1000-element Vector{Float64}:
0.5097500248005
0.514652524552495
0.5195059993069701
0.5143109393139004
0.5191678299207614
0.5239761516215538
0.5287363901053382
0.5334490262042848
0.5381145359422419
0.5327333905828194
0.5374060566769913
0.5420319961102213
0.5466116761491191
⋮
0.8043883364948524
0.7963444531299039
0.7983810085986048
0.7903971985126188
0.7924932265274927
0.7945682942622178
0.7966226113195956
0.7986563852063996
0.7906698213543356
0.7927631231407922
0.7948354919093843
0.7968871369902905Plotting the learning trajectory
Bibliographical remarks
Summary
- You’ve learned a few important concepts today:
- Grammar competition and variational learning
- How to sample objects according to a discrete probability distribution
- How to use conditional statements
- How to make a simple plot of a learning trajectory
- You get to practice these in the homework
- Next week, we’ll take the model to a new level and consider what happens when several variational learners interact