Intro to ABMs

Agent-based modelling, Konstanz, 2024

Henri Kauhanen

9 April 2024

What is an agent-based model (ABM)?

• No rigorous definition (like most applied science)
• But: can characterize as a model consisting of
  1. entities (the agents)…
  2. …which act¹ upon each other…
  3. …in some kind of environment…
  4. …to create some emergent outcome
• “Emergent” = collective is more than the sum of its parts
• Implemented computationally, sometimes also analysed mathematically

1. Eng. agent < Lat. agens, pres. part. of ago ‘act’

What is the benefit of ABMs?

“Like equation-based modeling, but unlike prose, agent-based models must be complete, consistent, and unambiguous” (Gilbert 2020, xii, my emphasis)

• complete: the modeller cannot leave anything out of the model description
• consistent: no part of the model can logically contradict another part of the same model
• unambiguous: the meaning of every part of the model must be objectively clear

What is the benefit of ABMs?

“Like equation-based modeling, but unlike prose, agent-based models must be complete, consistent, and unambiguous if they are to be capable of being executed on a computer” (Gilbert 2020, xii, my emphasis)

• complete: the modeller cannot leave anything out of the model description
• consistent: no part of the model can logically contradict another part of the same model
• unambiguous: the meaning of every part of the model must be objectively clear

Examples

These concepts are best explained through the use of examples…

…so let’s look at a few!¹

1. The examples are taken from the Example Zoo of the Agents.jl package (released under the MIT license).

Example 1: Conway’s Game of Life

• Early example of a cellular automaton (Gardner 1970)
• Lattice; each cell either “live” (L) or “dead” (D)
• Rules:

Rule	Cell	Neighbourhood	Result
“underpopulation”	L	< 2 L cells	L \(\to\) D
“sustenance”	L	2 or 3 L cells	L \(\to\) L
“overpopulation”	L	> 3 L cells	L \(\to\) D
“reproduction”	D	3 L cells	D \(\to\) L

Question

Earlier we said ABMs are complete, consistent and unambiguous.

What have I left out of the definition of Conway’s Game of Life? (I.e. why is my description so far incomplete?)

Question

Answer

Three very important things (at least):

1. Is the lattice finite or infinite? If finite, then what happens at the boundaries? – It is infinite.
2. Are the agents (the cells) updated synchronously (all at once) or asynchronously? – Synchronously.
3. How are a cell’s neighbours defined? – It’s the 8 cells surrounding it.

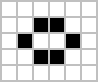
Exercise

What happens to the cells in A? What happens to those in B? (Black = live, white = dead)

A

B

Exercise

Answer

A is stable, B oscillates:

A

B

Species

The game supports many life forms (“species”), categorized into:¹

• Still lifes, e.g. 

• Oscillators, e.g. 

• Spaceships, e.g. 

1. Images of Game of Life species from Wikimedia Commons (public domain).

Emergence

• The game has simple rules, complex behaviour
• It is undecidable: given a starting state S and a proposed other state O, we can prove that it is impossible to prove whether O will ever be reached from S!
• New facts about the game are still being discovered: 2018 discovery of “knightships” (spaceships that move like the knight in chess)

Example 2: Flocking

Example 2: Flocking

• A simple model of the emergence of collective behaviour, flocking in birds¹
• Birds follow three rules:
  1. Collision avoidance: maintain a minimum distance to other birds
  2. Tracking: fly towards the average position of neighbouring birds
  3. Navigation: fly in the average direction of your neighbours

1. Reynolds (1987), and much research thereafter, importantly Vicsek et al. (1995) and subsequent.

Example 3: Social Distancing

• SIR (susceptible-infected-recovered) models are used to model epidemics, e.g. the spread of viruses¹
• Such models can be extended with aspects such as social distancing – implemented here as agents which remain stationary
• In the following animations,
  • black dot = susceptible (healthy) individual
  • red dot = infected individual
  • green dot = recovered individual

1. See Vynnycky and White (2010) for an overview.

Bounded rationality / Locality

• Common to all these examples is the following observation: the agents have bounded rationality
  • In Flocking, individual birds follow only three simple rules defined over the bird’s neighbours
  • A bird does not know what flocking means, nor does it have a rule to accomplish flocking
  • Rather, flocking emerges as the collective behaviour of a group of birds
• In other words, global patterns arise from numerous local interactions
• Similar remarks apply to Game of Life and Social Distancing, indeed to any ABM

Challenges in ABM

• How do we know what to model?
• How do we test our models against empirical data?
• How do we implement our models computationally?

Challenges of computational implementation

• Speed: we want simulations to be fast
• Randomness: when our code calls for random numbers, we want them to be really random!
• Cleanliness: we want our code to be understandable to other users
• Reproducibility: when others run our code, they should get the same results we do

Why is speed an issue?

• Central processing units (CPUs) in modern computers carry out billions of instructions each second
• However, with ABMs, computational requirements may be significant, and may not scale nicely

Example/Exercise

• Assume:
  • You have a model such that one simulation run, with a given set of parameter values, takes 1 minute to complete.
  • Your model has 2 parameters, each of which can assume 100 different values.
  • You want to replicate the simulation for each parameter combination 100 times for statistical reasons.
• How long will it take for your entire simulation to complete?

Example/Exercise

Answer

2 parameters with 100 values each results in 100 x 100 = 10,000 parameter combinations. Thus, in total, we have 100 x 10,000 = 1 million simulation runs to complete. If each run takes 1 minute, the total is 1 million minutes. This corresponds to roughly 2 years!

How to deal with issues of speed

1. Choose a suitable programming language
2. Write performant code
3. Whenever possible, parallelize your code
   • This means running it simultaneously across many CPUs/computers; we will see later how it’s done

Why is randomness needed?

• Quite simple: real-world processes are complex, and to model such complex processes we resort to stochastic processes
• A stochastic process is a sequence of random variables
• For example, consider a “navigating” agent that turns into a random direction whenever it doesn’t know how to proceed otherwise. In this case, the random direction needs to be generated using a random number.
• Or consider a linguistic example: suppose Mary is friends with Bob, Fiona and Charles. Unless we want to claim that Mary’s interactions with the other people are deterministic (which does not seem particularly sensible), we need some way of selecting interlocutors at random.

Why is randomness an issue?

• Conventional computers are deterministic devices
• So, if we need, say, a random number between 0 and 1, how is that accomplished?
• The answer is a pseudorandom number generator (PRNG)
  • This is an algorithm that generates a (long, but not infinite!) sequence of numbers which has the appearance of being random
  • The sequence is generated from a seed number. If you give the PRNG the same seed, you will get the same “random” sequence of numbers (this takes care of the reproducibility requirement).
  • However, there are significant issues…

Issues with PRNGs

• Suppose your PRNG generates a sequence of 1M numbers…
• …but in your simulation you need to generate 10M random numbers¹
• Then your “random” numbers will repeat 10 times
• This means that different parts of your simulation are not independent of each other – a major problem!
• Further issues can arise when we look at parallel processing… but more on that later!

1. We’ll see later that this is by no means a crazy requirement!

Summary

• ABM is a powerful framework for modelling real-world processes
• Models are complete, consistent and unambiguous
• Individual agents exhibit bounded rationality
• Challenges involve, among other things, simulation speed and proper implementation of randomness

The scientific community

• ABMs are created and explored by people in all manners of disciplines from physics and chemistry to linguistics and economics
• Examples of professional organisation in social sciences and linguistics:
  • European Social Simulation Association
  • The Journal of Artificial Societies and Social Simulation
  • The International Society for Computational Social Science (+IC2S2 conference)
  • Language Dynamics and Change (journal)

Homework

Next week, we will begin programming. To prepare your computer for this, complete the homework “Installing Julia” on the course website.

References

Gardner, Martin. 1970. “The Fantastic Combinations of John Conway’s New Solitaire Game ’Life’.” Scientific American 223 (4): 120–23. https://doi.org/10.1038/scientificamerican1070-120.

Gilbert, Nigel. 2020. Agent-Based Models. Second edition. London: SAGE.

Reynolds, Craig W. 1987. “Flocks, Herds and Schools: A Distributed Behavioral Model.” ACM SIGRAPH Computer Graphics 21 (4): 25–34. https://doi.org/10.1145/37402.37406.

Vicsek, Tamás, András Czirók, Eshel Ben-Jacob, Inon Cohen, and Ofer Shochet. 1995. “Novel Type of Phase Transition in a System of Self-Driven Particles.” Physical Review Letters 75: 1226–29. https://doi.org/10.1103/PhysRevLett.75.1226.

Vynnycky, Emilia, and Richard G. White. 2010. An Introduction to Infectious Disease Modelling. Oxford: Oxford University Press.